Setting up and using printers

Computations are at the heart of symbolic mathematics systems, but very often presentation and visualization of results or intermediate steps is also very important, for example for sharing results. SymPy implements a very generic and flexible framework for implementing printers of mathematical expressions, Python’s data types and date structures, and foreign types.

Built-in printers

There are many ways how expressions can be printed in Sympy.

Standard

This is what str(expression) returns and it looks like this:

>>> print x**2
x**2
>>> print 1/x
1/x
>>> print Integral(x**2, x)
Integral(x**2, x)

Note that str() is by design not aware of global configuration, so if you for example run bin/isympy -o grlex, str() will ignore this. There is another function sstr() that takes global configuration into account.

Low-level

Due to internal implementation of Python, SymPy can’t use repr() for generating low-level textual representation of expressions. To get this kind of representation you have to use:func:\(srepr\)

>>> srepr(x**2)
Pow(Symbol('x'), Integer(2))

>>> srepr(1/x)
Pow(Symbol('x'), Integer(-1))

>>> srepr(Integral(x**2, x))
Integral(Pow(Symbol('x'), Integer(2)), Tuple(Symbol('x')))

repr() gives the same result as str():

>>> repr(x**2)
x**2

Note that repr() is also not aware of global configuration.

Pretty printing

This is a nice 2D ASCII-art printing produced by pprint():

>>> pprint(x**2, use_unicode=False)
 2
x
>>> pprint(1/x, use_unicode=False)
1
-
x
>>> pprint(Integral(x**2, x), use_unicode=False)
  /
 |
 |  2
 | x  dx
 |
/

It also has support for Unicode character set, which makes shapes look much more natural than in ASCII-art case:

>>> pprint(Integral(x**2, x), use_unicode=True)
⌠
⎮  2
⎮ x  dx
⌡

By default pprint() tries to figure out the best of Unicode and ASCII-art for generating output. If Unicode is supported, then this will be the default. Otherwise it falls back to ASCII art. User can select the desired character set by setting use_unicode option in pprint().

Python printing

>>> print python(x**2)
x = Symbol('x')
e = x**2
>>> print python(1/x)
x = Symbol('x')
e = 1/x
>>> print python(Integral(x**2, x))
x = Symbol('x')
e = Integral(x**2, x)

LaTeX printing

>>> latex(x**2)
x^{2}
>>> latex(x**2, mode='inline')
$x^{2}$
>>> latex(x**2, mode='equation')
\begin{equation}x^{2}\end{equation}
>>> latex(x**2, mode='equation*')
\begin{equation*}x^{2}\end{equation*}
>>> latex(1/x)
\frac{1}{x}
>>> latex(Integral(x**2, x))
\int x^{2}\,dx

MathML printing

>>> from sympy.printing.mathml import mathml
>>> from sympy import Integral, latex
>>> from sympy.abc import x
>>> print mathml(x**2)
<apply><power/><ci>x</ci><cn>2</cn></apply>
>>> print mathml(1/x)
<apply><power/><ci>x</ci><cn>-1</cn></apply>

Printing with Pyglet

This allows for printing expressions in a separate GUI window. Issue:

>>> preview(x**2 + Integral(x**2, x) + 1/x)

and a Pyglet window with the LaTeX rendered expression will popup:

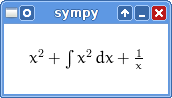
Setting up printers

By default SymPy uses str()/sstr() printer. Other printers can be used explicitly as in examples in subsections above. This is efficient only when printing at most a few times with a non-standard printer. To make Python use a different printer than the default one, the typical approach is to modify sys.displayhook:

>>> 1/x
1/x

>>> import sys
>>> oldhook = sys.displayhook
>>> sys.displayhook = pprint

>>> 1/x
1
─
x

>>> sys.displayhook = oldhook

Alternatively one can use SymPy’s function init_printing(). This works only for pretty printer, but is the fastest way to setup this type of printer.

Customizing built-in printers

Suppose we dislike how certain classes of expressions are printed. One such issue may be pretty printing of polynomials (instances of Poly class), in which case PrettyPrinter simply doesn’t have support for printing polynomials and falls back to StrPrinter:

>>> Poly(x**2 + 1)
Poly(x**2 + 1, x, domain='ZZ')

One way to add support for pretty printing polynomials is to extend pretty printer’s class and implement _print_Poly method. We would choose this approach if we wanted this to be a permanent change in SymPy. We will choose a different way and subclass PrettyPrinter and implement _print_Poly in the new class.

Let’s call the new pretty printer PolyPrettyPrinter. It’s implementation looks like this:

from sympy.printing.pretty.pretty import PrettyPrinter
from sympy.printing.pretty.stringpict import prettyForm

class PolyPrettyPrinter(PrettyPrinter):
    """This printer prints polynomials nicely. """

    def _print_Poly(self, poly):
        expr = poly.as_expr()
        gens = list(poly.gens)
        domain = poly.get_domain()

        pform_head = prettyForm('Poly')
        pform_tail = self._print_seq([expr] + gens + [domain], '(', ')')

        pform = prettyForm(*pform_head.right(pform_tail))
        return pform

def pretty_poly(expr, **settings):
    """Pretty-print polynomials nicely. """
    p = PolyPrettyPrinter(settings)
    s = p.doprint(expr)

    return s

Using pretty_poly() allows us to print polynomials in 2D and Unicode:

>>> pretty_poly(Poly(x**2 + 1))
    ⎛ 2          ⎞
Poly⎝x  + 1, x, ℤ⎠

We can use techniques from previous section to make this new pretty printer the default for all inputs.

Tasks

1. Following implementation of PolyPrettyPrinter, add a printer for Lambda which would use mapping notation (arrow) instead of lambda calculus-like notation.

   (solution)

2. Following the way how Poly is printed by str() printer, make PolyPrettyPrinter print domain including domain= string.

   (solution)

Implementing printers from scratch

SymPy implements a variety of printers and often extending those existent may be sufficient, to optimize them for certain problem domain or specific mathematical notation. However, we can also add completely new ones, for example to allow printing SymPy’s expression with other symbolic mathematics systems’ syntax.

Suppose we would like to translate SymPy’s expressions to Mathematica syntax. As of version 0.7.1, SymPy doesn’t implement such a printer, so we get do it right now. Adding a new printer basically boils down to adding a new class, let’s say MathematicaPrinter, which derives from Printer and implements _print_* methods for all kinds of expressions we want to support. In this particular example we would like to be able to translate:

• numbers
• symbols
• functions
• exponentiation

and compositions of all of those. A prototype implementation is as follows:

from sympy.printing.printer import Printer
from sympy.printing.precedence import precedence

class MathematicaPrinter(Printer):
    """Print SymPy's expressions using Mathematica syntax. """
    printmethod = "_mathematica"

    _default_settings = {}

    _translation_table = {
        'asin': 'ArcSin',
    }

    def parenthesize(self, item, level):
        printed = self._print(item)

        if precedence(item) <= level:
            return "(%s)" % printed
        else:
            return printed

    def emptyPrinter(self, expr):
        return str(expr)

    def _print_Pow(self, expr):
        prec = precedence(expr)

        if expr.exp == -1:
            return '1/%s' % (self.parenthesize(expr.base, prec))
        else:
            return '%s^%s' % (self.parenthesize(expr.base, prec),
                              self.parenthesize(expr.exp, prec))

    def _print_Function(self, expr):
        name = expr.func.__name__
        args = ", ".join([ self._print(arg) for arg in expr.args ])

        if expr.func.nargs is not None:
            try:
                name = self._translation_table[name]
            except KeyError:
                name = name.capitalize()

        return "%s[%s]" % (name, args)

def mathematica(expr, **settings):
    """Transform an expression to a string with Mathematica syntax. """
    p = MathematicaPrinter(settings)
    s = p.doprint(expr)

    return s

Before we explain this code, let’s see what it can do:

>>> mathematica(S(1)/2)
1/2
>>> mathematica(x)
x

>>> mathematica(x**2)
x^2

>>> mathematica(f(x))
f[x]
>>> mathematica(sin(x))
Sin[x]
>>> mathematica(asin(x))
ArcSin[x]

>>> mathematica(sin(x**2))
Sin[x^2]
>>> mathematica(sin(x**(S(1)/2)))
Sin[x^(1/2)]

However, as we didn’t include support for Add, this doesn’t work:

>>> mathematica(x**2 + 1)
x**2 + 1

and very many other classes of expressions are printed improperly. If we need support for a particular class, we have to add another _print_* method to MathematicaPrinter. For example, to make the above example work, we have to implement _print_Add.

Tasks

1. Make Mathematica printer correctly print \(\pi\).

   (solution)

2. Add support for Add and Mul to Mathematica printer. In the case of products, allow both explicit and implied multiplication, and allow users to choose desired behavior by parametrization of Mathematica printer.

   (solution)

Code generation

Besides printing of mathematical expressions, SymPy also implements Fortran and C code generation. The simplest way to proceed is to use codegen() which takes a tuple consisting of function name and an expression, or a list of tuples of this kind, language in which it will generate code (C for C programming language and F95 for Fortran, and file name:

>>> from sympy.utilities.codegen import codegen

>>> print codegen(("chebyshevt_20", chebyshevt(20, x)), "F95", "file")[0][1]
!******************************************************************************
!*                      Code generated with sympy 0.7.1                       *
!*                                                                            *
!*              See http://www.sympy.org/ for more information.               *
!*                                                                            *
!*                       This file is part of 'project'                       *
!******************************************************************************

REAL*8 function chebyshevt_20(x)
implicit none
REAL*8, intent(in) :: x

chebyshevt_20 = 524288*x**20 - 2621440*x**18 + 5570560*x**16 - 6553600*x &
      **14 + 4659200*x**12 - 2050048*x**10 + 549120*x**8 - 84480*x**6 + &
      6600*x**4 - 200*x**2 + 1

end function

In this example we generated Fortran code for function chebyshevt_20 which allows use to evaluate Chebyshev polynomial of the first kind of degree 20. Almost the same way one can generate C code for this expression.

Tasks

1. Generate C code for chebyshevt(20, x).
2. Make SymPy generate one file of Fortran or/and C code that would contain definitions of functions that would allow us to evaluate each of the first ten Chebyshev polynomials of the first kind.